【数学が苦手なあなたへ】原因の解明と克服する方法を提案｜具体抽象トレーニング（要約）

こんにちは、たっきーです！たきログは、本の学びと知識を共有しています。

本日は『数学が苦手な理由とその克服法』について。

あなたのそんな悩みを解決します。

この記事は『「具体⇔抽象」トレーニング 思考力が飛躍的にアップする29問』（細谷 功 著）を参考にしています。先日、要約記事を公開しました。

今回は本の知識を応用し、数学嫌いの要因をメタ視点から解剖します。

それでは、早速いきましょう！

数学が苦手な理由

数学が苦手な理由３選

数学が苦手な学生の心境は、主に次のようなものです。

これら３つの状態が堂々巡りすることで、数学嫌いのスパイラルにはまっていきます。

ありがちな数学の克服法

数学の苦手克服法としてよく挙げられるのは、以下の方法です。

思わず学生さんからこのような声が聞こえてきそうですね。しかし先生も親も塾講師もたいていは同じことをおっしゃるでしょう。

大人でも「ダイエット中にお菓子を食べてしまう」ことがあるように、そもそも嫌いなことを継続することは苦痛でしかありません。

根本的な問題解決（苦手の始まりを考える）

では、先ほど述べた「勉強してもわからない」「問題が解けない」「楽しくない」、これらの３つの状態はなぜ起こるのでしょうか？

それは「自分が今、全体のどの地点にいるのか分からないこと」からスタートしています。つまり「数学の何が分からないのかが分からない」のです。

そこで、まずは「数」の特性を知ることが始めましょう。

数学は抽象概念の学問である（具体抽象トレーニングより）

前提知識として『「具体⇄抽象」トレーニング』をおさらいします。

先の記事で解説したとおり、知的能力とは次の図で示されます。

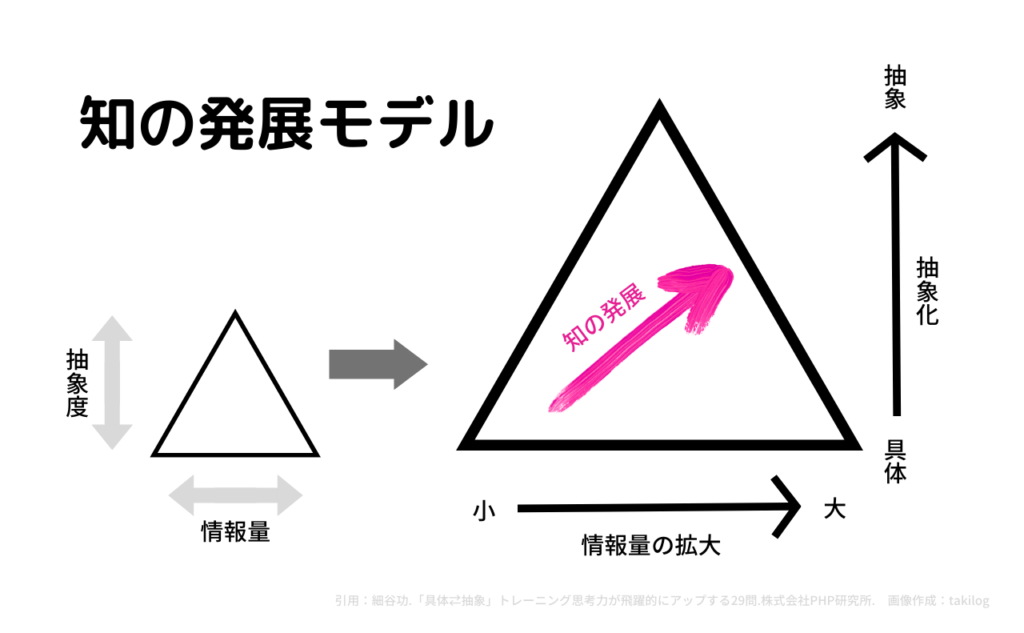
知的能力の向上には「情報量の量的拡大」だけでなく、「具体化や抽象化による質的拡大」が重要です。
簡単にいうと、頭の良さとは「つまり〜（抽象化）」や「例えば〜（具体化）」といった考え方によって向上していきます。

科目で分けるならば英語や歴史など、暗記で対応できる学問は横軸である「情報量の量的拡大」の分野です。そのため学年が上がっても難易度はあまり変わりません。

対して「数学」は、縦軸「抽象化の質的拡大」の学問です。

そのため学年が上がるについて抽象度が増していき、「自分が地図上のどこにいるかわからない状態」となりやすい。まさに「積み上げ式の学問」といえます。

積み上げ式の学問は一度分からなくなるとついていけなくなるため、脱落者が多いのが特徴です。

数学の苦手を根本的に克服する方法

そこで今回提案する克服法は、以下の２つです。

順に解説していきます。

克服法① 「数」を地図で確認し、自分が学んでいる位置を把握する

数学とは、はじめは「リンゴが何個あるか？」という現実世界から始まります。（＝自然数）
この時点では視覚を使って数えることができるため、つまづく人は少ないでしょう。

次にその「自然数」が、「0（リンゴがない）」や「負の数（＋と反対に進んだ数）」を含む「整数」の一部であったことを学習します。

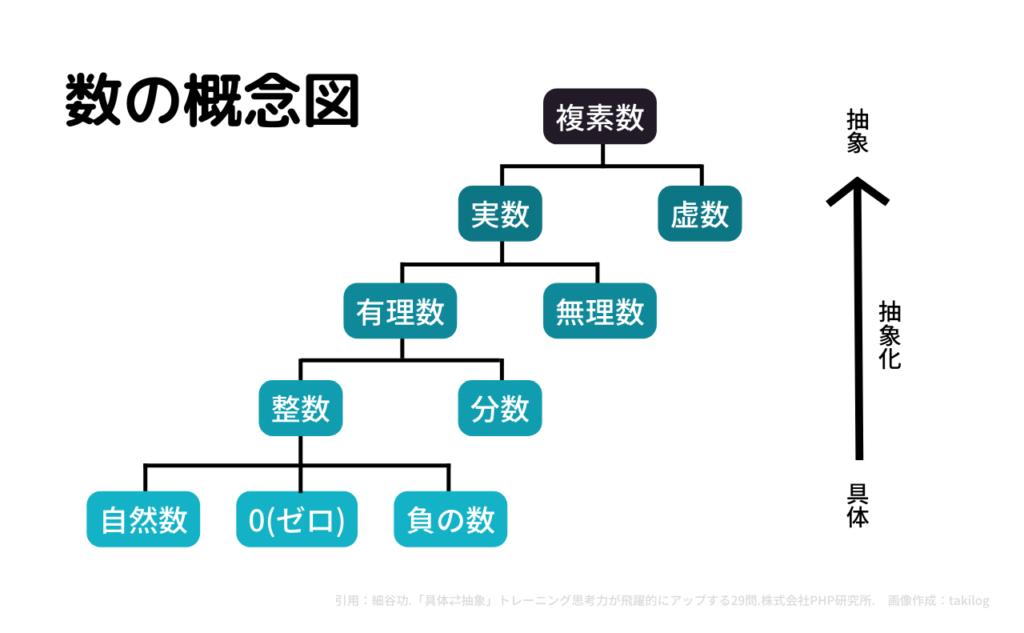
その後「整数」の間を表す数字として「分数」が生まれ、分数と整数をまとめて「有理数」と表現されます。

さらに円周率πやネイピア数e、√2などの”分数では表せない数”を「無理数」とし、２つをあわせて「実数」（実際にあると確かめた数）となります。

その後、現実には存在しない「虚数」（二乗して0未満の実数になる数）と「実数」の組み合わせを「複素数」として定義すれば、「数」という地図の完成です。

見ての通り、概念図の上方へ向かうにつれて抽象度が増すため、理解できる人が減っていくのは当然のこと。

このような抽象概念の学問においては、いかに現実世界に落とし込むかが「勉強のできる・できない」を分けていきます。「自分がどこにいるのか」を概念図で視覚的に捉えることも、「落とし込む」作業のひとつです。

あなたが今つまづいているのは、どの地点でしょうか？

理解できなくなった場所の、下位概念から再スタートしよう。
（下に行くにつれて現実世界に近く、イメージしやすい数である）

克服法② 「数」を現実世界に落とし込む

あなたは「ネイピア数 e」聞いて、なにが思い浮かぶでしょうか？

ネイピア数とは、実は私たちの生活に非常に関わりのある数なのです。

case. ネイピア数 e を考える

「ネイピア数 e 」は 2.71828… という謎の数字ではなく、ヤコブ・ベルヌーイという数学者が「複利の計算」から生み出したものです。

複利とは投資や家のローン、クレジットカードの分割払い、リボ払い、銀行の利息と、かなり身近にある考え方です。またアインシュタインが「人類最大の発明」と呼んだことも有名な話ですね。（詳しくはこちら）

たとえば「１年間預けると利息が 100% 増える銀行に、１万円を預けた」とします。
すると１年後には、倍の２万円になって返ってきます。

では半年で一度区切ると、１年後に貰える額は同じでしょうか？

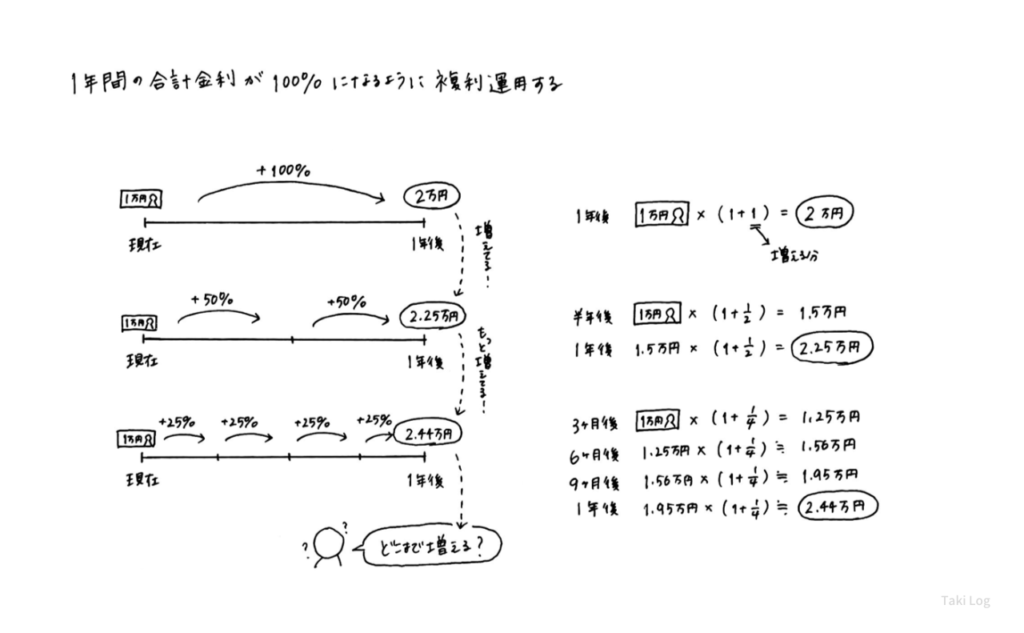
「半年で利息が 50% 増える」場合だと、１年後には 1.5×1.5 = 2.25倍 の 2.25万円 になり、先ほどの２万円よりも増えていることがわかります。（ 50% 増える＝1.5倍）

１年間の合計金利は同じ100%なのに、貰える額はなぜか期間を分けた方が増えているのです。

さらに「３ヶ月（1/4年）で利息が 25% 増える」場合だと、1.25×1.25×1.25×1.25 ≒ 2.44倍 の 2.44万円 です。（ 25% 増える＝1.25倍）また増えていますね。

どんどん細かく区切っていきましょう。

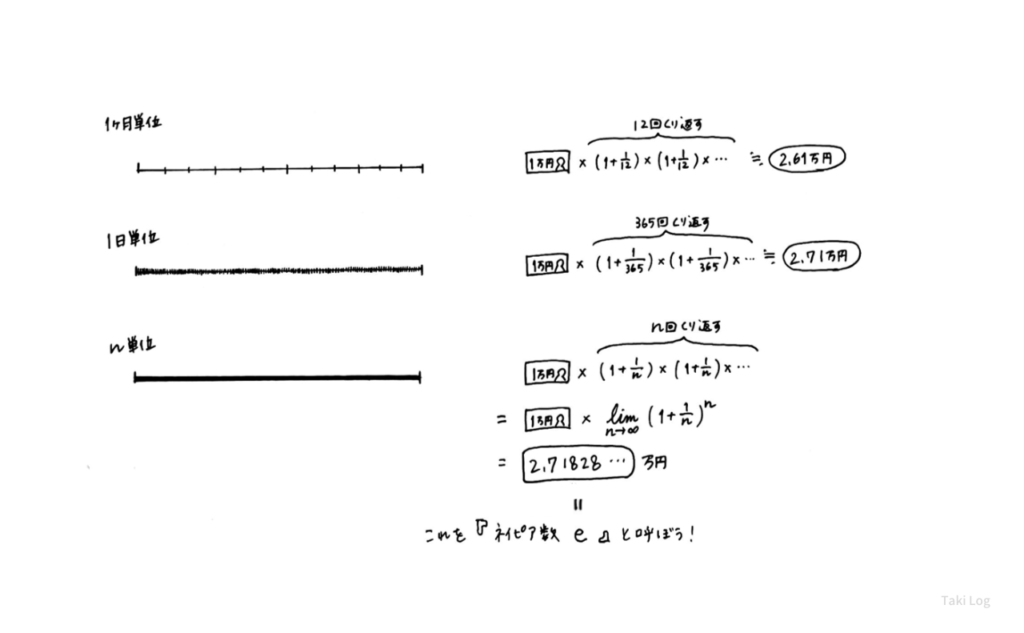
１ヶ月単位だと 「１ヶ月（1/12年）で利息が (1/12) 倍」なので、１年後には 2.61万円。
１日単位だと「１日（1/365年）で利息が (1/365) 倍」なので、１年後には 2.71万円。

ではこの期間を極限まで短い時間にしたとき、１年後にお金は何万円まで増えるのでしょうか？

実は、期間を極限まで短くした結果が 2.71828… となります。
これを『ネイピア数』と呼ぶことにしたのです。

数学が苦手な学生は、「ネイピア数 e = 2.71828…」とだけ頭に記憶します。

しかし「ネイピア数とはどこで使われる数字なのか？（How?）」と考えて具体まで落とし込むと、身の回りの複利を利用した現実社会と結びつき、ネイピア数が 「見えるようになります」。

このような数学の面白さを知ると、負のスパイラルから抜け出し「数学がわかる→すき」に変わっていくのです。

得体の知れない「数」は、現実社会と結びつければ「見えるようになる」。

おわりに

途方もない力は必要ない

人生において「好き」と「得意」がリンクしていると気づいたのは、社会人になってからです。

「好き」になるきっかけはあらゆるところに落ちています。ちなみに私が数学を好きになったのは、数学の先生に「解き方をほめられたから」でした。今思うと、たった一問、それだけです。

数学が社会にどう活かされているかを知りたいなら、ぜひ森岡毅さんの本を読んでください。
森岡毅さんとは、USJの経営危機をV字回復させた凄腕のマーケターです。

中学生にも分かるかんたんな計算しか使わないのに、圧巻の数学的思考法でUSJを立て直しています。